Che problema i problemi. Chi li risolve in un lampo e chi invece entra nella disperazione più nera. Calma e sangue freddo, dico io! Abbiamo ripassato, per tutto ottobre, addizione e sottrazione senza farci sfuggire niente. Le situazioni problematiche ci hanno accompagnato oralmente e come esempio per afferrare meglio i concetti affrontati. Ma arriva il momento di concentrarci proprio sulle procedure di risoluzione dei problemi. Sappiamo bene che non esiste un unico sistema e che ognuno poi ne troverà congeniale uno rispetto ad un altro. Ora alcuni problemi ci sembrano così semplici da poterli risolverle senza badare ai dati, scrivendoli o illustrandoli, senza usare diagrammi e addirittura andare in riga con l’operazione da svolgere. Ma se non acquisiamo subito un sistema per renderci i problemi meno complicati dobbiamo metterci all’opera. Con la mia classe ho deciso di iniziare proponendo una serie di strategie risolutive e sistemi pratici per focalizzare l’attenzione su dati, ragionamenti e procedure. Siamo partiti dalle consapevolezze emerse negli anni scorsi e abbiamo ripreso a costruire le nostre competenze.
Per riprendere in leggerezza la questione e non frustrare i bambini facendo scrivere fiumi di parole sul quaderno, ho deciso di utilizzare il software LIM del metodo analogico proposto per la classe quarta con i problemi per immagini. Sul metodo analogico, che ho utilizzato soprattutto per le strategie di calcolo e alcuni aspetti delle geometria e delle misure, devo spendere qualche parola. Intorno al metodo Bortolato ultimamente si è creato un nutrito dibattito. Devo ammettere che sono stata abbastanza critica sul metodo puro e sull’idea di Bortolato di matematica sin da subito. Per me il bello della matematica è proprio andar a capire come si sviluppa, quali ragionamenti ci sono alla base, le magie di arrivare ad un risultato anche prendendo strade diverse. Per Bortolato, diciamocelo chiaramente, è un automatismo. Certo, può magari (forse) funzionare per i bambini che non amano la matematica o hanno difficoltà da superare ma nelle lunghe distanze ho dei seri dubbi sul loro valore didattico. E le competenze? Insomma, io ho usato sino allo scorso anno gli strumenti di Bortolato che ho trovato interessanti e utili in certi momenti ma non ho mai abbandonato gli altri strumenti e gli altri metodi. Anche se con fatica (perché offrire vari strumenti costa sicuramente più fatica e nel breve tempo risultati più contenuti… gli automatismi funzionano bene e subito… ma poi?) posso dire di avere una classe con una mente abbastanza elastica e che nel tempo ha sviluppato strategie e capacità di sviluppare ragionamenti che, a mio avviso, sono fondamentali per intessere gli apprendimenti matematici futuri (e anche per appassionare alla matematica). Mi capita di intervenire in altre classi in cui molti hanno bei voti in matematica, bravissimi a risolvere operazioni in colonna e problemi in maniera automatica… ma quando si sposta la questione a ragionamenti o deduzioni o spiegazioni di cosa realtà ci sia dietro quel tanto calcolare e risolvere… mi ritrovo davanti a scene mute. Stessa cosa capita per le scienze, la geografia e la storia: tutti bravi a studiare a memoria ma poi basta una domanda che implica deduzione o ragionamento e crolla tutto. Io preferisco lavorare così sinceramente: non voglio automi ma sviluppatori di pensiero critico. Ne abbiamo davvero bisogno!
Tornando al metodo analogico, credo che siano molto interessanti i problemi per immagini. Ovviamente li uso come strumenti per sviluppare dei ragionamenti. Come ho avviato il discorso? Ho spiegato ai bambini che avrebbero dovuto usare il quaderno solo per segnare il riferimento del problema da risolvere e indicare esclusivamente l’operazione risolutiva. Alla LIM, con il software Matematica al volo in quarta con la LIM, ho proiettato il primo problema. La prima cosa che abbiamo fatto è stata osservare le immagini per capire la situazione, poi abbiamo individuato i dati nello schema e cercato anche di inventare oralmente una ipotetica situazione problematica. Infine ci siamo concentrati sulla domanda. Ogni bambino sul proprio quaderno ha risolto con l’operazione. Infine abbiamo confrontato le risposte e le soluzione e siamo andati avanti. Procedendo così siamo riusciti ad analizzare e risolvere circa una dozzina di problemi, scoprendo strategie, notando che per alcuni era possibile trovare soluzioni e strategie differenti e concentrandoci esclusivamente sul ragionamento. I problemi analizzati erano tipo questi (tratti dal libro sul Metodo Analogico che quest’anno i miei alunni non utilizzano) ma sul software risultano graficamente più belli, colorati e anche animati.
 Dopo aver giocato con i problemi per immagini in questo modo siamo passati allo step successivo: provare ad utilizzare questo sistema di ragionamento quindi imparare a schematizzare una situazione problematica. Ho precisato che ovviamente non tutte le situazione problematiche devono essere risolte così ma con il tempo saranno loro a scegliere la strategia migliore. Io stessa, quando devo risolvere situazioni complesse, talvolta utilizzo schemi o diagrammi, altre ho necessità di riportare i dati e analizzarli, altre ancora uso disegni (non parliamo poi dei problemi geometrici). Insomma: più sistemi acquisite… meglio è!
Dopo aver giocato con i problemi per immagini in questo modo siamo passati allo step successivo: provare ad utilizzare questo sistema di ragionamento quindi imparare a schematizzare una situazione problematica. Ho precisato che ovviamente non tutte le situazione problematiche devono essere risolte così ma con il tempo saranno loro a scegliere la strategia migliore. Io stessa, quando devo risolvere situazioni complesse, talvolta utilizzo schemi o diagrammi, altre ho necessità di riportare i dati e analizzarli, altre ancora uso disegni (non parliamo poi dei problemi geometrici). Insomma: più sistemi acquisite… meglio è!
Ho dettato loro un problema e chiesto di trasformarlo in problema per immagini utilizzando gli schemi acquisiti in precedenza. Loro hanno lavorato sul quaderno e io alla LIM ho raccolto le loro indicazioni. La consegna era: Scrivi il problema, illustra e risolvi.
Il testo era: Compero 3 vasetti di marmellata che costano 4 euro l’uno. Compero anche un vasetto di miele. Spendo in tutto 15 euro. Quanto costa il vasetto di miele?
Ovviamente tutti riescono semplicemente a risolvere il problema senza difficoltà utilizzando il modello acquisito. Rilancio con un altro problema ma questa volta dovranno lavorare completamente in autonomia. Questo sistema consente di affrontare i problemi in maniera più soft e meno faticosa ma allo stesso tempo permette di sviluppare strategie e ragionamenti. Quanto andiamo finalmente a lavorare sul libro scolastico è quasi un ripassare ciò che è stato acquisito. Sviluppiamo percorsi tenendo conto dei problemi con dati superflui o mancanti, affrontiamo i problemi impossibili o con dati incongruenti, riflettiamo sul significato di dati impliciti e espliciti. Ci addentriamo nei problemi a catena.
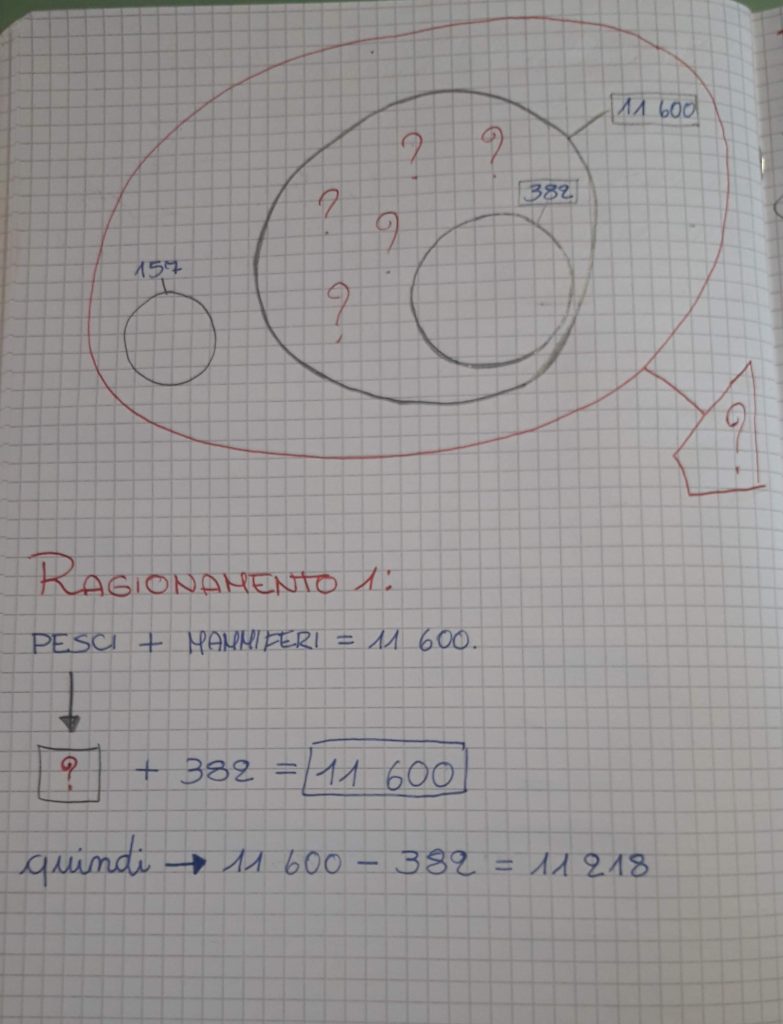
Propongo un problema che richiama l’argomento che stiamo sviluppando in scienze in questo periodo: gli ecosistemi. Per l’occasione ci trasferiamo al mare e ci occupiamo di fauna marina. Detto il problema, iniziamo a raccogliere i dati e analizzare la situazione. Ci concentriamo sui termini e il significato dei dati emersi. Ci rendiamo conto che sono posti due quesiti e che per risolverli avrò bisogno di fare qualche ragionamento in più. Spontaneamente ci viene in mente di utilizzare un diagramma di Eulero-Venn e richiamare i vecchi insiemi. Appena rappresentiamo alla lavagna il nostro insieme tutto appare più chiaro e come per magia riusciamo a risolvere serenamente il problema. Ecco com’è andata:
In questo caso abbiamo prestato attenzione alla raccolta dei dati e al loro significato. Inoltre abbiamo notato che per rispondere alla seconda domanda non era necessario risolvere il primo quesito… quindi non si trattava di dover ricavare dei dati. Per visualizzare meglio i dati esistenti e quelli da ricavare utilizzo dei semplici schemi risolutivi che consentono di comprendere immediatamente come operare. In questo caso, proprio come dovrebbe sempre essere, lo schema precede l’operazione. Ritengo assolutamente inutile il metodo spesso proposto tra i banchi di far scrivere lo schema dopo aver già individuato e risolto l’operazione. Lo schema, se utilizzato, deve aiutare ad arrivare alla soluzione e individuazione delle operazioni… diversamente è solo un passaggio inutile e forzato.
Dopo aver sviscerato varie situazioni problematiche riconduco il discorso all’utilizzo di addizione e sottrazione con due situazioni problematiche apparentemente simili ma dai procedimenti diversi. Per aiutarci a comprendere come fare mi aiuto con altre tipologie di schemi. Anche in questo caso lo schema mi aiuta a ragionare. Essendo problemi un po’ particolari che a primo acchito sembrano impossibili… “Bambini, la prima volta che l’ho letto ho iniziato a vederci doppio! Ma poi con calma ho capito come procedere”… ho ribadito quali passaggi fondamentali non dobbiamo dimenticare: leggere con attenzione il testo magari cercando di immaginare la situazione, analizzare i dati, focalizzare l’attenzione sulla domanda, scegliere una strategie risolutiva utile (magari scegliendo di illustrate, utilizzare un diagramma, ecc) e la/le operazione/i necessarie alla risoluzione. Non meno importante, stare attenti alle parole utilizzate nel testo. E infatti il nostro primo problema ci consente proprio di mettere a punto tutti questi consigli:
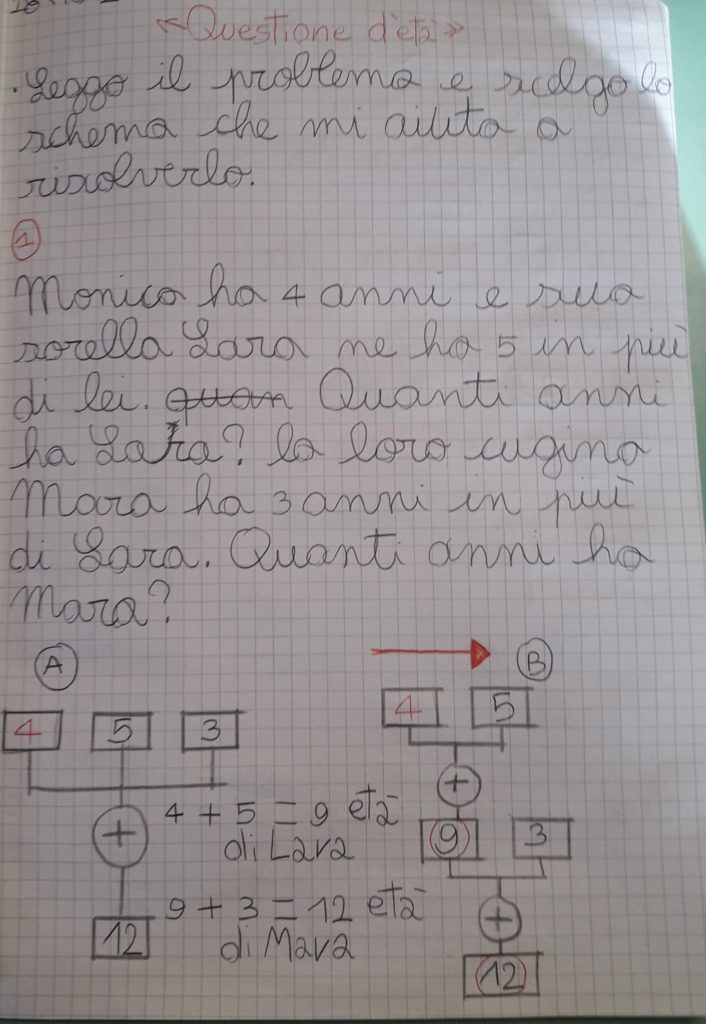
Monica ha 4 anni e sua sorella Lara ne ha 5 in più di lei. Quanti anni ha Lara? La loro cugina Mara ha 3 anni in più di Lara. Quanti anni ha Mara?
In questo caso lo schema è di grande aiuto. Propongo alla lavagna due schemi diversi. Loro dovranno indicare quale dei due rappresenta meglio il problema e ci consente di risolverlo senza intoppi e rispondendo a entrambe le domande. Nel primo caso, come noterete, la prima domanda non viene presa in considerazione mentre nel secondo caso abbiamo la possibilità di focalizzare l’attenzione su entrambe.
Il secondo problema gioca sempre con le età ma a differenza del problema precedente, in cui era necessario utilizzare l’addizione, in questo caso si procede con la sottrazione.
Mia nonna ha 68 anni e ha 29 anni in più di mia mamma, la quale ha 28 anni in più di me. Quanti anni ho?
Anche in questo caso propongo due schemi, inserendo due dati in ciascuno. Loro dovranno scegliere come risolvere il problema utilizzando lo schema giusto. Ecco lo schema risolutivo:
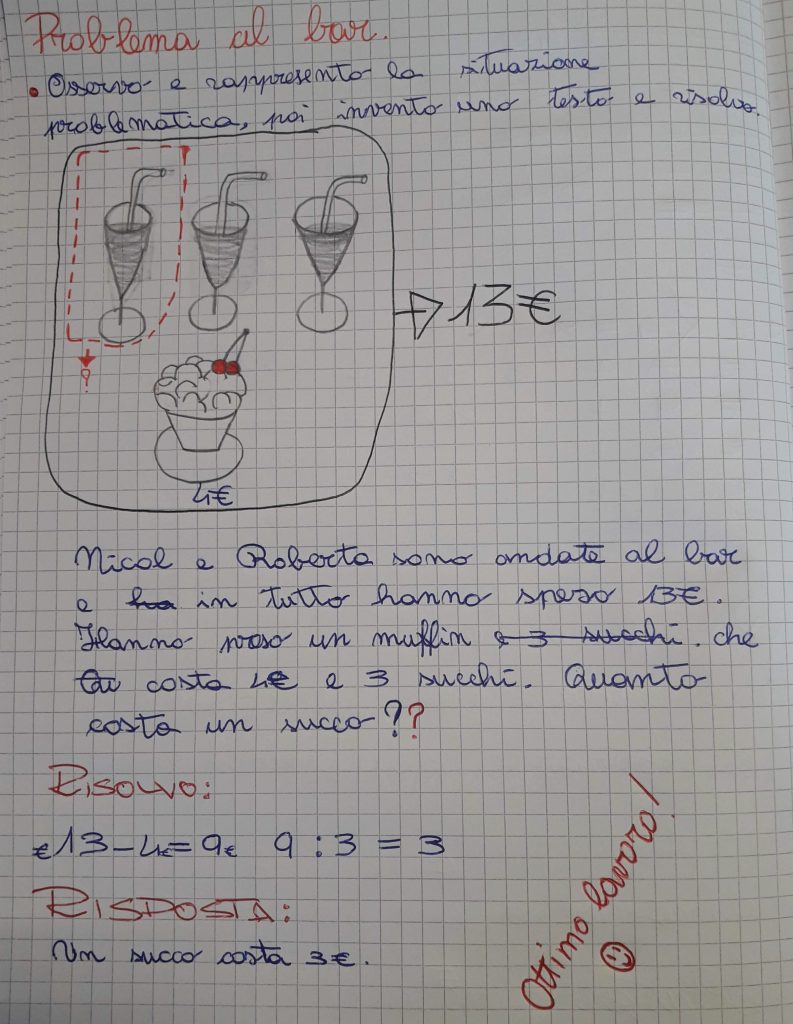
Concludiamo la prima parte sui problemi con una sfida: data una situazione problematica illustrata secondo gli schemi precedentemente utilizzati si cerchi di pensare e scrivere un testo problematico che infine andrà risolto. Alla LIM illustro la situazione, dopo aver spiegato bene la consegna, e i bambini infine ricopiano sul quaderno. Dopo aver ipotizzato un “racconto” di quanto potrebbe essere accaduto impostano il testo problematico e infine risolvono. Ecco l’esempio dal quaderno di un’alunna (ma le situazioni narrate sono davvero tante… alcune davvero buffe!!!):
Con la risoluzione di situazioni problematiche abbiamo avuto ancora una volta l’opportunità di riflettere sui concetti di unione, aggiunta e aumento per l’addizione e di rimanenza, differenza e complementarietà per la sottrazione. Le riflessioni collettive, il soffermarsi sui termini e sulle differenti possibilità di risoluzione ci hanno permesso di consolidare quanto appreso nel mese di ottobre. Il prossimo passo sarà il ripasso della moltiplicazione e della divisione. Novembre ci attende…