Evviva le bambine e i bambini belli! Quelli che non si fermano dietro ad una paura e non temono di alzare un dito durante la lezione per sollevare dubbi, incertezze o domande. Grazie alle loro domande e ai loro dubbi, grazie alla loro voce coraggiosa che si fa sentire anche per quelli che vorrebbero ma non riescono, grazie al loro non abbassare la testa ma essere fieri di coltivare spirito critico. La mia più grande soddisfazione è poter partecipare al desiderio impellente di un bambino che, alzando la mano durante la lezione di matematica, manifesta un dubbio, lo argomenta e cerca risposte. Il dubbio implica prima di tutto un interesse per quanto si sta apprendendo, presuppone uno studio e un coinvolgimento critico, sta alla base di domande generate da necessità, è la linfa vitale dell’osservazione critica e del procedere in maniera scientifica… oltre che filosofica. Niente di più esaltante. Cerco sempre di mettere positivamente in luce quei bambini e quelle bambine che sollevano dei dubbi davanti alla classe e chiedono spiegazioni. Non mi riferisco a chi alza la mano dopo una bella spiegazione e mi dice “non ho capito” magari perché nel frattempo pensava ad altro. Mi riferisco a quei bambini che con occhio vispo e sguardo attento, a tratti pensieroso, alzano la mano nel cuore di una spiegazione o di una correzione degli esercizi per manifestare un dubbio. Quando accade questa magia mi si drizzano le antenne… il mio sguardo si fa ancora più vitale e iniziano a prudermi le mani. “Maestra, posso chiederti una cosa… perché io su questo ho dei dubbi… perché…” e allora la fermo quella vocina timida ma tenace. Chiedo il silenzio e l’attenzione di tutti. Non solo la voce della maestra è quella da ascoltare con attenzione ma soprattutto quella dei compagni. La voce allora cerca le parole giuste per spiegare, ricorda esempi… mostra casi e prova a ipotizzare risposte che necessitano aiuti. A questo punto mi avvicino alla lavagna e gesso alla mano “Vediamo insieme come possiamo ragionare“… e lì inizia l’avventura. Quel dubbio, lo so, sarà una possibilità in più per molti. Un regalo prezioso che bisogna sfruttare. Evviva i dubbi!
MA perché tutto questo giro di parole? Beh, capita spesso di accogliere i dubbi dei miei alunni che oramai lo sanno: sono ben graditi! Ma venerdì scorso abbiamo avuto proprio un tripudio di dubbi e reazioni a catena esaltanti. Alla fine eravamo così felici e matematicamente (ma quindi anche umanamente e filosoficamente) vivi che ci è sembrato di vivere una mezz’ora con l’intensità di un giorno. Un momento di condivisione ed esaltazione collettiva in cui la lezione ha preso vita da loro e, poi, me che cercavo di snodare la matassa a partire dai loro dubbi e dalle loro risposte. Beh, amo insegnare matematica proprio per questo.
Venerdì abbiamo fatto una verifica sui grandi numeri, addizione e sottrazione (calcolo in colonna, proprietà e strategie di calcolo veloce). Molti bambini hanno terminato nel giro di una ventina di minuti quindi, per non disturbare gli altri, ho chiesto loro di prendere il libro di matematica e iniziare a leggere con attenzione le due pagine sulla moltiplicazione (argomento che avrei introdotto al termine della prova). Ovviamente si trattava di riprendere in mano il concetto di moltiplicazione (affrontato in seconda, sviluppato in terza e da approfondire quest’anno in quarta), ripassarlo e entrare nel vivo di alcuni aspetti: niente di nuovo sotto il sole. Quando finalmente tutti hanno concluso la prova, abbiamo iniziato a leggere a voce alta la prima pagina. 
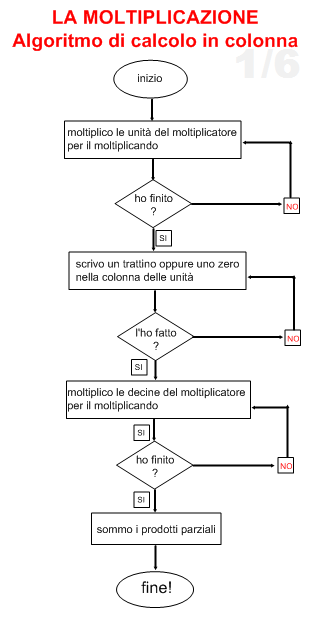Con la moltiplicazione, questa volta, ho deciso di partire dal libro, e poi sviluppare l’argomento alla LIM e sul quaderno su alcuni aspetti. Lunedì, ad esempio, vedremo l’algoritmo di calcolo della moltiplicazione, a partire da un bel diagramma a blocchi (ricollegandoci anche al discorso che stiamo sviluppando ultimamente in informatica su coding e pensiero computazionale), poi sviscereremo le proprietà e le strategie di calcolo sino ad arrivare a situazioni problematiche miste. Questa lezione introduttiva invece riprendeva quanto acquisito negli anni scorsi: moltiplicazione come addizione ripetuta, i termine della moltiplicazione, alcuni aspetti del calcolo in colonna e il valore dell’1 e dello 0 nella moltiplicazione. Sul significato della moltiplicazione tutto è filato liscio. Alla lavagna abbiamo fatto esempi mirati a partire da quanto letto sul libro, constatato similitudini tra addizione ripetuta e moltiplicazione, verificato differenze tra 3 x 4 o 4 x 3 (ad esempio) a seconda del significato attribuito a ciascun fattore. Nell’ovvietà siamo andati a cercare ancora una volta di capire perché è più comodo utilizzare la moltiplicazione quando un addendo si ripete tante volte. Ho scritto alla lavagna 3 + 3 + 3 + 3 e loro hanno subito convenuto che fosse più semplice calcolare 3 x 4 mettendo in luce che l’addendo 3 si ripeteva ben 4 volte. Differente invece il 4 x 3. Certo, il risultato non cambia ma se stiamo analizzando una situazione problematica e io devo capire quanti pasticcini avrò in tutto se riempio 4 vassoi con 3 pasticcini ciascuno è certo che sarà la quantità 3 (i pasticcini per vassoio in questo caso) che dovrò moltiplicare per il numero dei vassoi. “Al contrario maestra sarebbe 4 x 3 se avessi 3 vassoi in cui metto 4 pasticcini“. Sappiamo che il risultato comunque non cambia perché? Perché i bambini, come ben ricordano, sanno che anche nella moltiplicazione possiamo sfruttare la proprietà commutativa (come nell’addizione). Ricordo quindi che la moltiplicazione la possiamo usare se notiamo che uno stesso addendo si ripete. “Ma se per caso ce ne sono molti uguali e uno no, non posso usarla?” mi chiede un bambino. “Beh, nessuno ci vieta di sfruttare le potenzialità della moltiplicazione. Vediamo un esempio e poi mi dite come fareste” e scrivo 4 + 4 + 4 + 6 + 4 + 4 + 4.
Osservano attenti. “Quanti addendi vedete? – SEI – Alcuni di questi si ripetono? – CERTO – Per quante volte e cosa possiamo fare?” Il bambino che aveva posto la domanda prende la parola: “Possiamo fare 4 x 6… e poi quell’altro addendo… il 6 lo aggiungiamo dopo”. Scrivo e in effetti anche gli altri sono d’accordo. Ma un altro compagno alza il tiro: “Però se io immagino quel 6 come fatto da 4 + 2… magari a questo punto posso fare 4 x 7 e poi + 2!” I conti tornano e il ragionamento non fa una piega anzi… direi che è ottimo. Stiamo lavorando nel campo delle strategie di calcolo e questa cosa di scomporre i numeri e riunirli come se fossero delle costruzioni è interessante e divertente, oltre che renderci le cose più semplici. Facciamo altri esempi e ci togliamo dei dubbi. Senza questa domanda forse avrei dovuto impostare una lezione apposita su questo aspetto o magari sarebbe rimasta nel dimenticatoio delle cose fatte sul libro e poi dimenticate. Adesso, in questo modo, son certa che sia stata metabolizzata dalla maggior parte di loro.
Il libro ci offre un altro spunto di riflessione – grazie a un dubbio sollevato da un’alunna – con la moltiplicazione in colonna a due cifre per entrambi i fattori, un qualcosa che io avevo dato per scontato in effetti perché mi sembrava banale. Vediamo quindi la prima moltiplicazione (24 x 15) e fila tutto liscio anche quando leggiamo accanto “dobbiamo considerare solo il risultato totale e non fare caso ai parziali”. A me sembrava una cosa scontata e banale e non mi ci sono neanche soffermata. Accanto proseguiamo con la prova della moltiplicazione applicando la proprietà commutativa (15 x 24) e constatando che il risultato in effetti non cambiava. Ma alza la mano una bambina e ammette che questo aspetto le aveva sempre creato dubbi “Io risolvevo la moltiplicazione ma poi nella prova andavo sempre a guardare anche i risultati parziali ed erano diversi… allora temevo di sbagliare… e mi veniva da ricopiarli per paura che poi il risultato non tornasse“. In effetti non possono che essere diversi perché stiamo moltiplicando cifre diverse, invertite. Ma poi alla fine tutto torna, faccio io. Allora alza la mano un’altra bambina “Sì, ma non capisco per quale motivo visto che i fattori son sempre quelli. Come può succedere“. Quando si spiega la moltiplicazione si procede a piccoli passi e utilizzando anche gli strumenti che ci consentono di sviscerarne i perché (ricordo di averlo sviluppato con BAM e anche abaco per mostrare loro cosa accadesse con decine e unità (e in modo particolare con il trattino da metter sotto le unità o lo zero da aggiungere al secondo passaggio) ma c’è da dire che in quella fase molti bambini sono più interessati alla procedura: è nuova, sembra complicata, è lunga. La loro attenzione è rapita dal comprendere il meccanismo per operare in colonna, l’algoritmo di calcolo. Ora, con la serenità e la tranquillità di saper svolgere l’operazione sorgono i dubbi: ci si pone domande. Prendiamo il gesso, vado alla lavagna e evidenzio con pazienza cosa accade. Nel primo caso sto ripetendo il numero 15 x 4 unità (ottenendo 60) e a questo dovrò aggiungere il secondo parziale che ottengo ripetendo sempre il 15 ma per 2 decine (300). Il mio risultato sarà infatti 360. Nella prova faccio qualcosa di diverso: moltiplicherò il 24 per 5 unità ed è ovvio che il primo prodotto parziale sarà un numero diverso da 60 (ossia 120) come lo sarà il secondo (24 x una decina) ossia 240. Il finale sarà comunque 360 rispettando la proprietà commutativa. Si tira un sospiro di sollievo.
Il dubbio più grande però spunta fuori con i numeri moltiplicati per zero e quindi con il valore assorbente dello zero nella moltiplicazione. Mano alzata “Maestra, io lo so che ogni numero che moltiplico per zero mi deve dare zero… ma io non riesco proprio a capire il perché. Nell’addizione io ho una quantità, aggiungo zero (che non è niente) e quindi è come se non avessi aggiunto niente. Riscrivo quel numero. Ma perché nella moltiplicazione no? Io non sto moltiplicando per niente… ma quella cifra ce l’ho comunque! E allora perché diventa zero?” La questione dello zero è sempre spinosa e allora, preso nuovamente il gesso (quel giorno lì avevo deciso malauguratamente di usare i pantaloni neri… e non vi dico come ero ridotta a fine lezione ahahaha) inizio a dirigermi alla lavagna dicendo “Sullo zero non è facile ragionare perché di per sé immaginare il valore zero è difficile. Se dico 1 riuscite a immaginare quella quantità – posto che di quantità poi si tratti eh… ma noi spesso abbiamo bisogno di concretezza – e anche se dico 100… a grandi linee ve ne fate una ragione. Con lo zero vi viene da pensare che significa niente e allora che ci sia o meno non cambia niente. Credo che il concetto di zero in matematica sia difficile da digerire proprio come il concetto d’infinito. Ma per farvi capire il significato dello zero in matematica mi aiuto con un esempio che in realtà vi avevo fatto quando in seconda vi avevo spiegato il significato della moltiplicazione… anche con lo zero“. Ora io non ho le immagini della lavagna, che in quella giornata, nella foga, ho cancellato mille volte e quindi vi racconterò utilizzando un foglio che ho qui nel mio tavolo da lavoro. Un pomeriggio Giulia e Silvia decidono di giocare insieme a casa di Silvia. Cerco di rappresentare la situazione in modo matematico aiutandomi con gli insiemi: disegno un insieme che rappresenta la bambine che giocheranno (un insieme che contiene 2 elementi). Le due bambine decidono di giocare con le bambole. Ne hanno a disposizione 3. Decidono di utilizzarne una alla volta e poi di scambiarsele. Quindi disegno l’insieme bambole che contiene 3 elementi e poi con le frecce di colori diversi mi aiuto spiegando via via che prima Giulia gioca con la bambola X e Silvia con quella Z; poi Giulia con la Y e silvia con la X; infine Giulia con la Z e Silvia con la Y. “Beh, quante possibilità di scambio possono avere? Lo calcoliamo come?” Rispondono che possiamo fare comodamente 2 x 3. In questo caso non stiamo calcolando le combinazioni possibili.
Prese una alla volta le 3 bambole per le 2 bambine ottengo 6 possibili combinazioni (o coppie) diverse.
Per loro è chiaro (lo ricordavano dalla seconda classe). Ma mettiamo il caso che quel giorno il papà di Silvia abbia messo in lavatrice le 3 bambole… Lascio intatto l’inseme della bambine (che contiene due elementi) e “svuoto” quello delle bambole. “Quanti elementi contiene adesso l’insieme delle bambole disponibili per giocare? – ZERO! – Quante possibilità di scambio possiamo operare? – ZERO! Neanche una!!!“. Esattamente così: 2 x 0. Il 2 resta, le bambine son sempre lì… ma a noi interessa scoprire quante sono le possibilità non quante bambine o bambole ci sono. Se fosse stata una sola bambola quante possibilità avrebbero avuto? Solo 2: nella prima la utilizza solo Silvia e nella seconda solo Giulia. Ma nel caso dello 0 non abbiamo possibilità alcuna… bisognerà giocare con le macchinine! “Ma maestra… ma se aggiungo zero?” Stai però aggiungendo… cambia tutto. Abbiamo 2 (le bambine) aggiungo che cosa? Le bambole? Quante? 3? Ok, ma ottengo 5 cosa? Cinque bambine no… come neanche 5 bambole. Cinque elementi … certo… ma questo è un altro problema: non abbiamo neanche l’addizione ripetuta. Cambia ogni cosa. Se siete a giocare tu e Silvia e vengono a trovarvi Martina, Mara e Sofia allora possiamo dire che siete 2 + 3 ossia 5 ma non ha niente a che fare con la questione bambole. Se le bambole sono solo 3 quante possibilità di scambio avrete? Beh, soltanto 15 possibilità di scambio. “Finalmente ho capito e ora che ci penso capisco anche perché quando calcolo la moltiplicazione in colonna sbaglio: mi confondo e mi viene sempre da non mettere 0 ma riscrivere il numero moltiplicato per 0! In automatico mi viene da pensare all’addizione ma non è così affatto“.
Dopo questa condivisione molti sembrano più sollevati e, mossi dall’entusiasmo sollevano altre questioni… aggiungono spunti… offrono contributi: si sentono protagonisti della lezione. Io ringrazio le mie alunne coraggiose facendo loro i complimenti per aver avuto la forza e l’intelligenza di sollevare questi dubbi: solo grazie a loro molti dei dubbi silenti dei compagni… sono stati spazzati via. “Non crediate di essere le uniche ad avere dubbi. Molti non hanno la forza per domandare pensando erroneamente di mostrarsi poco preparati. E invece io ho grande stima di chi solleva dubbi e questioni perché mi dimostra entusiasmo e curiosità partecipata. E poi grazie ai dubbi si sono sviluppate le scienze e per fortuna sono esistiti scienziati pieni di dubbi che per risolverli hanno fatto scoperte fondamentali! Quindi complimenti a voi che siete entrate perfettamente nello spirito scientifico per eccellenza!“.
Ci saremo potuti far scivolare sopra questa paginetta di ripasso in dieci minuti (tempo di lettura intensa di quella pagina eh) ma invece siamo riusciti a costruirci sopra, grazie alle mie alunne (e forse anche grazie alla mia attenzione nel cogliere al balzo questa opportunità), una brillante e utilissima lezione. S’impara molto di più in questo modo che in mille pagine di quaderno scritte per automatismo. Questo è il tempo invisibile, quello che dedichiamo fuori dal quaderno…, che non si vede agli occhi dei genitori, ma che è il più prezioso. E io sono rientrata a casa con il sorriso.
Nella mia IV B si lavora sempre così! 🙂
Il ripasso sulla moltiplicazione è proseguito attraverso la presentazione di una serie di moltiplicazioni di vario tipo. Ci siamo prima concentrati su quelle senza riporto e tutto è filato liscio. Poi abbiamo preso in considerazione quelle con il riporto (scegliendo moltiplicazioni con “tabelline semplici” in modo da restar concentrati sul procedimento). Ho proposto alcune moltiplicazioni dal software Matematica al volo in quarta e i bambini hanno lavorato sul quaderno. Una volta finito il lavoro individuale ho chiamato alla lavagna per la correzione correttiva e l’analisi dell’algoritmo di calcolo e delle difficoltà emerse. In questo modo è stato possibile discutere su alcuni dubbi ancora presenti come, ad esempio, la questione riporti (qualcuno tendeva a tenerli fissi e sommarli a quelli successivi… chissà perché?) o i dubbi sullo zero (non metterlo come segna posto oppure sì). Ho ripreso alcune spiegazioni e ne ho offerte altre suggerendo strategie per memorizzare il procedimento come automatismo oppure come ragionamento (e quindi cercando di capire la necessità del riporto come dello zero segnaposto… che ha un suo significato specifico come abbiamo visto precedentemente). Poi ci siamo dedicati alle moltiplicazioni con gli zeri presenti nei fattori e la difficoltà a gestirli rischiando di confondersi con quelli segnaposto. infine abbiamo affrontato moltiplicazione a difficoltà mista.
Dopo questo ulteriore ripasso ci siamo immersi nel mondo delle proprietà e delle strategie di calcolo. “Tenete presente che queste proprietà le usate già da tempo e sono utili proprio perché vi facilitano i calcoli” Per me è molto importante che i bambini acquisiscano le proprietà in modo da poterne trarre vantaggio magari evitando ogni volta di andare in colonna. La colonna, infatti, dovrà essere utilizzata se necessaria. Se riusciamo a calcolare in riga sfruttando le strategie acquisite senza dover ricorrere alla colonna… tanto di guadagnato.
Per tutto novembre continueremo a lavorare con la moltiplicazione (comprese alcune situazioni problematiche di rinforzo con addizione e sottrazione insieme) per poi dedicarci, da dicembre, alla divisione.
