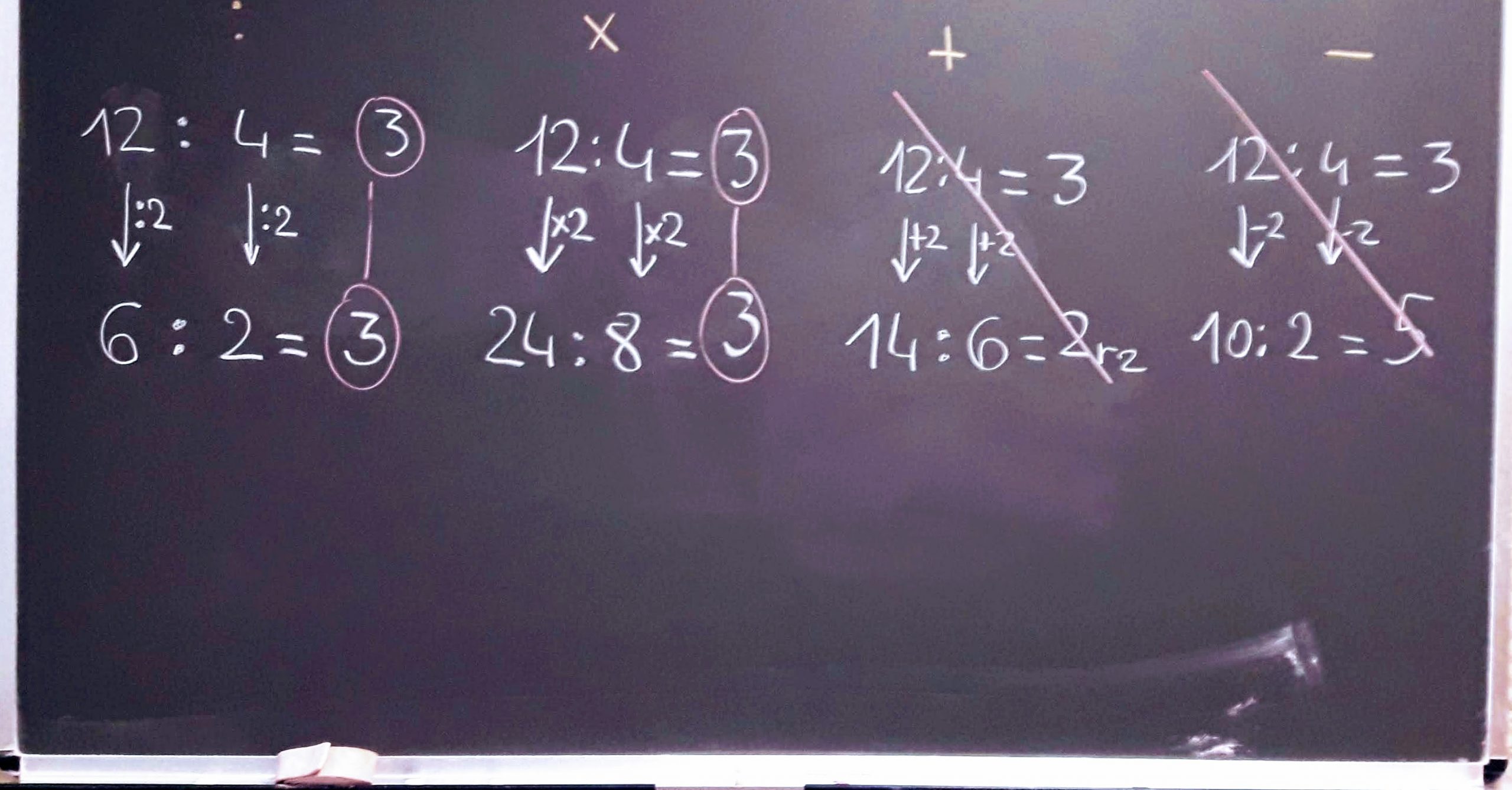Il lavoro con la moltiplicazione si è concluso in maniera positiva: abbiamo lavorato con il calcolo in riga, esplorando strategie e ripassando le proprietà, e anche in colonna, acquisendo l’algoritmo di calcolo e consolidando le tabelline. Ci siamo resi conto che se non è necessario ci conviene adottare le strategie di calcolo veloce piuttosto che andare a lavorare in colonna e, giocando con gli schieramenti e i problemi per immagini, abbiamo compreso quando la moltiplicazione può esserci utile. Nelle nostre ore di attività e discussione condivisa abbiamo spesso ritenuto necessario richiamare addizione e sottrazione ma anche divisione, sino ad allora non ancora chiamata in causa. Ho deciso di utilizzare proprio un semplice esercizio di moltiplicazioni per introdurre nuovamente la divisione ampiamente affrontata lo scorso anno. Ho chiesto ai bambini di inserire il fattore mancante di alcune moltiplicazioni in riga in cui era presente anche il risultato. Per arrivare alla soluzione è stato necessario richiamare alla memoria la divisione. Infatti osservando gli esempi presentati alla LIM i bambini hanno subito intuito come operare:

Per poter risolvere la consegna , i bambini hanno lavorato in maniera inversa ricordando anche che la prova della divisione è proprio la moltiplicazione. Così, facilmente, sono riusciti a lavorare in serenità. Ho insistito affinché ripetessero la frase chiave “Qual è quel numero che moltiplicato per 2 fa 12? Il 6” e così inserivano. Questa frase è esattamente la stessa che lo scorso anno utilizzavamo per risolvere le divisioni in riga e in colonna. Dopo aver lavorato in questo modo, ho chiesto di trasformare le moltiplicazioni nella loro operazione inversa e quindi ricavare delle divisioni. Hanno indicato (come da esempi sopra) 12: 2 = 6 ; 28 : 4 = 7… ecc.
Una volta riportato alla memoria il procedimento per eseguire semplici divisioni in riga ci siamo dedicati al significato della divisione. Lo abbiamo fatto con due semplici problemi molto simili ma dal significato diverso. Nel primo problema (UN FIORAIO DEVE CREARE CON 48 ROSE DELLE COMPOSIZIONI UGUALI IN 6 VASI. QUANTE ROSE METTE IN CIASCUN VASO?) si trattava di ragionare sul significato di divisione come distribuzione. Ho scelto un problema semplice in modo che la classe potesse concentrarsi sul ragionamento e il concetto senza lo stress dei calcoli. Il secondo problema (CON 48 ROSE IL FIORAIO DEVE PREPARARE DEI MAZZI DA 8 ROSE CIASCUNO. QUANTI MAZZI RIESCE A CONFEZIONARE?) è un caso di divisione che raggruppa. I problemi molto simili ci hanno consentito di ragionare ancora una volta su significati diversi della divisione. Solo a questo punto abbiamo preso il nostro libro di testo e letto con attenzione gli aspetti riguardanti la divisione, rendendoci conto che quanto proposto era un ripasso di quanto appreso in terza. Abbiamo osservato che ogni numero diviso per 1 dà come risultato se stesso mentre ogni numero diviso se stesso dà come risultato 1. Abbiamo invece scoperto che dividere un numero per 0 è impossibile in quanto sappiamo che qualunque numero moltiplicato per 0 dà sempre 0.
Dopo aver visto le prime divisioni semplici in colonna mi son resa conto che molti bambini avevano delle titubanze, come era ovvio che accadesse, e quindi ho proposto loro una serie di divisioni in colonna dal software LIM del metodo analogico. Queste divisioni prendono in considerazione le tabelline (dalle più semplici sino alle più ostiche) in un crescendo di difficoltà. I bambini operavano sul quaderno e di volta in volta venivano ad eseguire, a turno, a voce alta alla lavagna. In questo modo i bambini attenti al posto hanno avuto modo di memorizzare ancora di più l’algoritmo di calcolo. In questa fase sono basilari alcuni aspetti: l’ascolto e l’attenzione nella fase del lavoro, una buona conoscenza delle tabelline, una meccanicità nell’esecuzione dell’algoritmo di calcolo favorita dagli esercizi. Le attività di consolidamento a casa sono importanti e consentono di far capire quali siano dubbi e perplessità come di affinare quanto acquisito con la pratica in aula. Per consolidare ulteriormente i calcoli con la divisione (ma senza dimenticare le altre operazioni affrontate) e i suoi significati, ho proposto alcuni problemi per immagini del software LIM Metodo Analogico. Alla LIM ho proiettato i problemi e i bambini sul quaderno hanno indicato le operazioni e i calcoli risolutivi. Questo tipo di problemi consente di mantenere la concentrazione sulla situazione problematica senza lo stress della scrittura e della lettura del testo (faticoso soprattutto per i bambini DSA). Ogni problema, risolto individualmente sul quaderno, è stato corretto alla lavagna tenendo conto di diverse possibilità di soluzione, di strategie di calcolo adottate e della possibilità di imbastirci una storia sopra. Nel giro di poco tempo siamo riusciti a risolvere tanti problemi e ripassare molti aspetti riguardanti questa operazione… che fa un po’ paura.
Il lavoro sulla divisione continua sondando alcune strategie di calcolo veloce a partire da una situazione problematica. Ci immedesimiamo in una situazione verificatasi a scuola alcuni giorni prima per comprendere meglio dati del problema e domanda:

Questa volta utilizziamo i colori per sottolineare i dati e la domanda. Riportiamo con precisione i dati e ragioniamo passo per passo sull’importanza di trovare le parole giuste che ci possono aiutare a capire quali operazioni eseguire per scoprire il dato da trovare (la domanda del problema). Capiscono immediatamente sarà opportuno calcolare quanti sono gli alunni presenti (22 -2 = 20) in modo da procedere poi nel calcolo della distribuzione. Ragioniamo insieme sul significato di “distribuire” e impostiamo l’operazione (120 : 20). Non avendo ancora lavorato con le divisioni e a due cifre al divisore (che introdurrò solo quando tutti saranno sicuri nell’operare in colonna con il divisore a una cifra) chiedo di trovare una strategia che ci consenta di risolvere ugualmente riducendo i due termini e in modo particolare far diventare il divisore a una cifra. “Maestra possiamo togliere quello zero da una parte e dall’altra!” Intuizione ottima ma come possiamo tradurre questo “togliere uno zero” in termini matematici? Riportando alla memoria prassi già acquisite (ripassate anche quando abbiamo rivisto i numeri moltiplicati per 10, 100 e 1000) qualcuno propone di dividere entrambi i termini per 10. In effetti si tratta proprio di applicare la proprietà invariantiva della sottrazione che, come tutte le proprietà, ci aiuta a lavorare in maniera semplificata e senza ricorrere alla colonna. A questo punto calcolare 12:2 è semplicissimo e con facilità otteniamo il risultato e la risposta al quesito posto dal problema. Decidiamo così di cavalcare l’onda, e ricordandoci anche la proprietà invariantiva della sottrazione, cerchiamo di ricavare quanto dice: Il risultato della divisione non cambia se entrambi i termini sono moltiplicati o divisi per uno stesso numero. “Guardate bene cosa ho scritto alla lavagna: moltiplicati o divisi… stesso numero… entrambi i termini. Nelle proprietà prendiamo sempre in riferimento entrambi i termini e lo stesso numero ma in questo caso possiamo dividere o moltiplicare. Verifichiamo se funziona? Proviamo anche a applicare la proprietà aggiungendo o sottraendo e verifichiamo?“. Alla lavagna propongo delle divisioni semplici ma efficaci per verificare quanto abbiamo stabilito:
In effetti è proprio quanto stabilito dalla proprietà: addizionando o sottraendo il risultato della divisione cambia!
Propongo una serie di divisioni da semplificare applicando la proprietà invariantiva. Scopriamo che quando ci sono degli zeri conviene sempre dividere per 10 oppure troviamo strategie per trovare il divisore da applicare. In questo modo ripassiamo alcuni dei criteri di divisibilità scoperti lo scorso anno e che, in questa fase sono estremamente utili. I bambini ricordano che se un numero è pari può essere sempre diviso per 2 oppure se termina con lo 0 o il 5 può essere diviso per 5. Se termina con lo 0 può essere diviso per 10 e se le cifre che compongono il numero, sommate, danno un numero divisibile per 3 (135 ad esempio: 1 + 3 + 5 = 9 che è un numero divisibile per 3 come lo è l’intero numero). Tenendo conto di questi aspetti risulta molto semplice trovare uno stesso divisore da applicare ai due termini in modo da semplificare i calcoli notevolmente. Prima di Natale abbiamo ancora diverse lezioni per continuare a lavorare con il calcolo in colonna (e verificare anche le competenze acquisite), affinare le strategie di calcolo (divisioni per 10, 100 e 1000) e approfondire il discorso dei divisori (e anche dei multipli). Al rientro dalle vacanze probabilmente sarà il momento di affrontare le nostre prime divisioni a due cifre al divisore!