Basta le solite pizze e torte per presentare le frazioni! Mi ribello. Anche perché, diciamocelo… chi di voi riesce davvero a dividere in parti uguali torte e pizze? Siamo pratici… usiamo la carta piuttosto. Non sarò originale ma almeno consento ai miei alunni ad operare immediatamente in maniera matematica. Il nostro libro di testo sforna velocemente una pizza e in tre misere pagine liquida le frazioni. Certo, se ne riparlerà nei prossimi anni… però il lavoro più grosso dobbiamo impostarlo noi insegnanti. Chissà perché ma insegnare le frazioni mi ha sempre stimolato, forse per la grande trasversalità che offre questo tipo di attività: numeri, geometria, l’orologio, i decimali.
Prima di tutto mettiamo in luce quali siano gli obiettivi da raggiungere in classe terza:
- discriminare interi frazionati e non
- riconoscere interi frazionati e quantificarne le parti
- riconoscere e denominare unità frazionarie
- individuare i termini di una frazione
- individuare la frazione che rappresenta parti di una figura geometrica data
- individuare in una figura geometrica la parte corrispondente a una frazione data
- confrontare e ordinare frazioni, utilizzando i simboli >, < e =
- acquisire il concetto di frazione complementare
Ovvio, gli obiettivi e i tempi in cui raggiungerli dipendono sempre dalla classe che guidiamo.
Discriminare interi frazionati e non
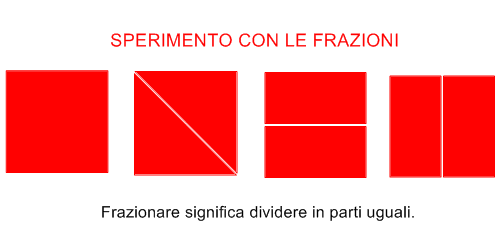
Ricollegandomi ad un’attività presentata alcuni giorni prima – calcolare la metà e la terza parte di un numero -, ho chiesto ai bambini di prendere un foglio quadrato da me predisposto e dividerlo in due parti uguali. Alla LIM ho disegnato un quadrato scomponibile in due parti usando tre criteri: dividerlo per la diagonale; dividerlo con una linea orizzontale; dividerlo con una linea verticale. Questo tipo di esperimenti, affrontati anche lo scorso anno con le simmetrie, sono di facile intuizione e applicazione. Dobbiamo far notare ai bambini che quello è un foglio intero che noi vogliamo dividere in parti uguali. Dopo aver piegato il foglio e verificato che le due parti combaciassero perfettamente abbiamo ritagliato con le forbici. Alla LIM abbiamo raccolto le informazioni in questo modo:
Con la LIM è molto semplice manipolare le figure e in questo modo possiamo fare tanti esempi senza rischiare di sbagliare ma soprattutto poterli rivedere in caso di necessità. Allo stesso tempo i bambini possono manipolare con la carta e poi incollare il tutto sulla pagina del loro quaderno per tenerne traccia. Facciamo notare ai bambini che le due parti ritagliate sono congruenti perciò sovrapponibili e pertanto uguali. “Bambini, possiamo affermare che le due parti dell’intero che abbiamo diviso sono uguali? Possiamo dire di aver diviso questo intero in due parti uguali? Ecco, possiamo dire di aver operato una frazione“. Da queste considerazioni cerchiamo di capire cosa significa frazionare: dividere un intero, o anche una quantità (come vedremo in seguito) in parti uguali. In questo caso il nostro intero è una forma quadrata. Passiamo subito dopo ad una forma non facilmente divisibile in due parti uguali: “Adesso dividete questa forma in due parti… come preferite“. Pieghiamo, ritagliamo e dividiamo. Lavoriamo alla LIM e sul quaderno in questo modo:
E alla fine traiamo le conclusioni. Lavoriamo in questo modo con tanti esempi aiutandoci anche con i disegni.
Svolgiamo un semplice esercizio di riepilogo che ci consente di comprendere se abbiamo appreso quanto emerso e se siamo in grado di discriminare gli interi frazionati da quelli che non lo sono. Come primo passo va molto bene. Faccio notare ai bambini che è fondamentale comprendere questa distinzione. Dopo aver frazionato i nostri interi chiedo ogni volta un feed back: “L’intero è stato frazionato? In quante parti? Cosa abbiamo ottenuto?”. Inizialmente tendevano a chiamare le parti “mezzi” ma poi abbiamo notato che i mezzi riguardano solo gli interi divisi in due parti (le così dette metà) quindi via via abbiamo scoperto altri nomi interessanti. Gli interi non frazionati invece li abbiamo divisi semplicemente in parti chiamate così, senza nome specifico. Qualche bambino ha risposto che l’intero era stato diviso in… due interi! e questo ci ha dato modo di riflettere su un aspetto interessante: l’intero corrisponde a una unità. E’ uno. Se lo divido in parti uguali ottengo parti più piccole o più grandi di quell’intero? – Ovviamente più piccole… e varranno meno di uno, no? Non possono essere altri interi… visto che sono parti di quell’intero. Per questo le chiamiamo PARTI FRAZIONATE (cioè divise in parti uguali). Ogni parte (unità frazionaria più piccola dell’intero) è più piccola dell’intero stesso. “Ma vi faccio riflettere ancora. Noi adesso stiamo operando in maniera concreta… ossia stiamo manipolando quantità che riusciamo a vedere perché sono rappresentate da figure e possiamo, con la matita o con le forbici, dividerle e vedere come diventano. Ma la matematica spesso è astratta… quindi dobbiamo fare uno sforzo straordinario per utilizzare numeri che rappresentano quantità che non riusciamo a manipolare concretamente. Pensate a quando fate una divisione tipo questa: 3460 : 2. In questo caso non prendiamo 3460 palline e le dividiamo in due parti uguali… devo usare i numeri. Se io ho la quantità 12 da dividere ad esempio in 3 parti uguali… riesco a farlo, giusto. 12 può rappresentare qualsiasi cosa… ad esempio 12 figurine. Questo 12 è un intero secondo voi? Sì, 12 figurine… ciascuna delle quali è un’intero, una unità… se vogliamo. Se io divido la quantità 12… (una decina e 2 unità) ottengo una quantità più piccola: 3… ossia tre unità. Sono ancora interi. Sto lavorando ancora nel campo dei numeri interi. Ma se io ho una quantità pari a 1, ad esempio… e la devo dividere in due parti uguali… otterrò ancora un numero intero?“. Alcuni bambini ipotizzano soluzioni… dicendo che sarà la metà di uno… ma quanto è? Sarà 0,1? Prediamo l’euro che ci aiuta subito. Una moneta da un’ero la consideriamo l’intero. Se voglio avere due monete uguali che sommate facciano un euro… cosa devo prendere? “Maestra, due da 50 centesimi!“. E così arrivano alla soluzione che 1:2 è uguale a 0,5. Certo, questa è un’altra storia – che vedremo a breve -, ma intanto capiamo che le frazioni operano con numeri che non sono più interi ma… con la virgola. “Si chiamano numeri decimali e vedremo tra qualche lezione… il perché“. Intanto conserviamo nella nostra testa questi ragionamenti e ricordiamoci perché un intero frazionato non ci può dare altri interi.
Riconoscere interi frazionati, quantificarne le parti e individuare unità frazionarie
Solo quando sono certa che tutti gli alunni riescono a distinguere gli interi frazionati da quelli che non lo sono posso procedere con la quantificazione delle parti. Utilizzo degli strumenti molto utili che presentano forme rettangolari e circolari già divise e con le parti frazionate già nominate. Permetto ai bambini di manipolare gli strumenti (colorati e in plastica trasparente) osservando e traendo delle conclusioni insieme ai compagni appartenenti alla stessa isola di lavoro. “Da quante parti è formato l’intero? Osservate la dicitura che viene utilizzata… e ditemi secondo voi cosa significa” Riprendo alla LIM uno degli esempi che hanno in mano e pongo domande mirate per far arrivare loro stessi alla soluzione.
L’intero è diviso in 4 parti e ogni parte e una parte di esso: 1 su 4. Arriviamo a definire l’unità frazionaria in modo molto semplice: ciascuna delle parti in cui una figura è frazionata si chiama unità frazionaria. Nel nostro caso si chiama un quarto e si scrive 1/4. Il numero che sta sotto la linea di frazione (si chiama così, faccio notare ai bambini) ci indica in quante parti è stato diviso l’intero mentre il numero che sta sopra indica le parti prese in considerazione e, nel nostro caso, ciascuna parte. “Quanti quarti abbiamo bambini? – Ne abbiamo 4! – E se li sommo? 1/4 + 1/4 + 1/4 + 1/4 cosa ottengo? – Otteniamo tutto l’intero!!” Arriviamo infatti a 4/4 che in termini differenti significa 4 parti su quattro. Ma c’è anche un ragionamento in più: la linea frazionaria sta a significare DIVISO e se io faccio 4 diviso 4 ottengo proprio 1 che è l’intero. Questi calcoli però li mettiamo da parte per ora (anche se sono molto interessanti da sviluppare) e andiamo con ordine. Prendiamo certamente anche questi appunti volanti, teniamoli a mente, perché ci serviranno per i ragionamenti futuri e ci rendiamo conto che per ora siamo a buon punto. Ci esercitiamo un po’ sul quaderno disegnando interi, nominando le parti e concentrandoci sulle unità frazionarie. Ecco il nostro lavoro sul quaderno:
Il prossimo passaggio sarà riuscire a individuare i termini di una frazione e iniziare ad operare con essa. Ci aspettano molte attività di sperimentazione, riconoscimento e conoscenza… sino ad arrivare al concetto di frazione complementare. QUI la seconda parte.