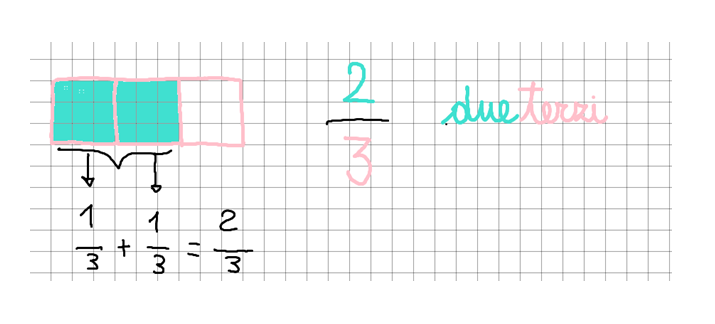Dopo aver introdotto il concetto di frazione e iniziato a ragionare sull’unità frazionaria ho suggerito ai bambini di rivedere a casa le pagine fatte sul quaderno e consolidare quanto affrontato insieme andando a svolgere le pagine del libro. In questo periodo lavoreremo soprattutto alla LIM e sul quaderno mentre il libro ci servirà per fissare nella nostra memoria, a casa, le esperienze fatte in aula. Abbiamo iniziato la nostra lezione con un esercizio di ripasso sull’unità frazionaria e questo mi ha consentito anche di chiamare alla lavagna i bambini assenti o i bambini ancora titubanti. Abbiamo proceduto prima insieme e poi ho lasciato loro il via libera. Di tanto in tanto sono sorte domande che ci hanno dato l’opportunità di ragionare anche su altre ipotesi: E se prendiamo più di una parte? Ma quell’unità frazionaria che prendiamo in considerazione è come l’unità che conosciamo? – Queste loro domande ci hanno portato a sviluppare il resto della lezione e a scoprire anche lo stretto legame tra frazioni e numeri con la virgola (così li chiamiamo per ora). Alla LIM comunque ho imposto l’esercizio in questo modo:
Ho chiesto loro di disegnare il primo intero rappresentandolo come una sorta di filo di perline. “Questa volta il nostro intero è diviso in quante parti? – Cinque! – E vi ricordate dove stiamo segnando ogni volta le parti in cui un intero è diviso?“. A questo punto faccio anche notare che sopra la linea di frazione stiamo indicando le parti prese in considerazione… che per ora sono sempre state equivalenti a 1. Nel primo esempio lavoriamo insieme, poi disegno gli interi alla LIM, loro ricopiano sul quaderno ed eseguono la consegna: colorare solo una unità frazionaria e poi nominare la frazione. Una volta che il lavoro sul quaderno è terminato chiamo un bambino alla volta alla LIM per correggere e verificare insieme.
Individuare i termini di una frazione, saper rappresentare e riconoscere frazioni
A questo punto passiamo al “matematichese” vero e proprio… ossia concentriamoci sui termini e sul linguaggio matematico. Riprendo l’esempio dei quarti affrontato nella lezione precedente e chiedo ai bambini di ricomporre l’intero avvicinando tra loro le varie parti e ricordando l’addizione tra quarti operata precedentemente. Faccio notare ai bambini che quando frazioniamo un intero il nostro punto di riferimento è una unità. Quella unità del quarto rappresenta la parte dell’intero che è stata divisa in 4 parti e che quindi è più piccola dell’intero stesso. Infatti le parti frazionate sono sempre più piccole dell’intero stesso. Questo ci porterà in seguito a ragionare coi numeri decimali e scopriremo proprio il valore delle parti. A questo punto continuiamo a lavorare con le figure frazionate ma prendiamo più parti rispetto al lavoro fatto con l’unità frazionaria. In questo caso i bambini iniziano a confrontare le frazioni e a intuire anche i valori. Se prendo una figura che è stata divisa in 6 parti e ne prendo in considerazione 2 e ne prendo un’altra che è stata divisa in 3 parti e ne prendo solo 1 mi trovo di fronte a frazioni equivalenti. Questi semplici ragionamenti consentono di acquisire una sorta di elasticità tra valori numerici e viene vissuta quasi come un gioco alla scoperta di quanto alla fine tutto torni 😉 Intanto però lavoriamo sul riconoscimento delle parti e sulla denominazione e scrittura delle frazioni. Sentiamo anche la necessità di dare un nome ai termini della frazione: numeratore (il numero che sta sopra la linea di frazione e che indica le parti prese in considerazione) e denominatore (il numero che sta sotto e indica le parti in cui è stato diviso l’intero). Con questo tipo di attività, ben presto, procederemo anche al confronto tra frazioni: ci aiuteremo soprattutto con i disegni e lo strumento in dotazione con la Linea del 1000. Sul libro di Bortolato ci sono inoltre una serie di esercizi molto semplici e di facile comprensione per operare i primi confronti tra frazioni e anticipare anche il concetto di frazioni complementari. Proporrò alla mia classe attività semplici e mirate che verranno approfondite in quarta. Nel nostro libro la frazione complementare non viene affrontata ma decido comunque di proporla perché ci arriviamo in maniera del tutto naturale e senza forzature. Per oggi comunque restiamo concentrati sui termini della frazione e sul riconoscimento delle frazioni stesse. Alla LIM lavoriamo passo passo insieme mentre sul quaderno prendiamo gli appunti che ci serviranno per ripassare o avere esempi del nostro lavoro.
Mi sposta alla lavagna nera per ragionare sull’unità divisa in tante parti uguali. Notiamo che sino ad ora abbiamo sempre lavorato con quantità pari a una unità o più grandi: decine, centinaia e migliaia. Adesso invece ci dobbiamo confrontare con numeri più piccoli. E siccome mentre con le quantità maggiori a uno riuscivamo ad operare anche senza dover per forza disegnare (perché tutti riescono a capire in cosa consiste una quantità pari a una decina… visto che ne abbiamo immediatamente anche l’immagine mentale) ora immaginare quantità più piccole di uno diventa complicato. Ed ecco che in questo ci aiutano le frazioni. Questo ragionamento lo sviluppiamo proprio prendendo in riferimento la decima parte dell’intero… la decima parte dell’unità. In questo caso comprendiamo bene che questa decima parte sarà più piccola di dieci volte l’unità. La decina è più grande dell’unità di dieci volte… mentre il decimo… è dieci volte più piccolo. Rispolverando i vecchi trucchi del moltiplicare per dieci spostandoci di uno zero (aggiungendolo) sulla destra e della divisione ossia spostandoci verso la sinistra (togliendolo) mostro il loro primo “spostamento” che fa spuntare fuori una virgola). Questo discorso verrà ovviamente affrontato a breve ma intanto semino qualcosa.
Finalmente ci concentriamo sui termini della frazione, proseguiamo andando avanti e utilizzando soprattutto i colori… che ci aiuteranno a memorizzare significati e nomenclature. La LIM è sempre di grande aiuto, anche perché la pagina la imposto io ma poi ci lavorano anche loro. Per presentare i termini della frazione però decido di fare il salto di qualità e introdurre una nuova componente: non più unità frazionarie.
Parto prima dalla frazione scritta e della nomenclatura delle parti, richiamando sempre alla memoria i significati emersi, e poi cerchiamo di immaginarci una possibile rappresentazione della frazione 2/3. Alla fine verifichiamo che tutto torni: un terzo più un terzo in effetti fanno due terzi. “Quanto manca per formare un intero? – Un terzo!“. Anche il concetto di frazione complementare, che loro ancora non conoscono, può essere dedotto con semplicità. Adesso si tratta di rinforzare con alcuni semplici esercizi quanto abbiamo visto. Il procedimento è sempre lo stesso e funziona: io propongo alla LIM, loro osservano e poi lavorano in autonomia sul quaderno, si corregge tutti insieme alla LIM in modo che vengano fatti subito dei riscontri.
Nei nostri esempi inserisco anche la frazione cinque quinti che mi consente di far notare ai bambini che si tratta in realtà dell’intero stesso: Ho un intero, l’ho diviso in 5 parti e ne prendo in considerazione 5… che sono tutte le parti, ossia l’intero. Alla lavagna nera facciamo alcuni esempi di questo tipo. Notiamo poi che 5 parti su 5 significa tutto l’intero (se pur frazionato) ma andiamo oltre: sapendo che la linea frazionaria non è altro che una divisione “Se io faccio 5 diviso 5 cosa ottengo? Esattamente 1. E torniamo all’intero!”
Sul finale lancio una sfida: “Ora prova tu a disegnare e nominare la frazione”. Lavorano un po’ in questo modo, ritiro i quaderni per correggere e loro continuano a lavorare ancora sulle frazioni nell’eserciziario confrontandosi infine con i compagni dell’isola di lavoro.
Una volta verificate le competenze acquisite sulle frazioni procederemo con le frazioni decimali, i numeri decimali e l’euro… che verranno affrontati di pari passo e in maniera concatenata. E aspetto con ansia di presentare a breve la Rana Romilda… Ma questa è un’altra storia! Se avrete un po’ di pazienza la presenterò anche a voi!
