Nei giorni scorsi ho introdotto il concetto di frazione decimale riagganciandomi al lavoro sulle frazioni svolto in precedenza e riprendendo il concetto di intero come valore unitario. Anche questa volta abbiamo lavorato step by step alla LIM e sul quaderno, andando di tanto in tanto alla lavagna nera per sviluppare ragionamenti o segnare appunti volanti (anche grazie al brainstorming), e consolidato infine con una semplice scheda tratta dalla Guida Unica classe Terza.
Prima di tutto ho richiamato alla memoria i concetti appresi nelle ultime lezioni e poi ho chiesto di disegnare un intero e di dividerlo in 10 parti uguali. Ho fatto presente che tutti i ragionamenti che avremmo fatto insieme avrebbero riguardato solamente gli interi divisi in 10 parti uguali (e in seguito divisi in 100 e 1000 parti uguali) e non invece tutti gli altri, ricordando loro che il nostro è un sistema decimale – come abbiamo sempre detto e notato in questi anni – e lo avremmo dimostrato ancora una volta.  Ho chiesto di prendere in considerazione solo una decima parte di quell’intero e di nominarlo. Dopo di che, andando alla lavagna nera, ho disegnato una linea dei numeri così come l’abbiamo sempre conosciuta: inizia da 0, prosegue in ordine crescente con numeri interi, potrebbe continuare all’infinito. “Ma vi siete mai chiesti cosa accade in quell’intervallo che va dallo 0 all’1? Noi lo vediamo. Ci sarà uno spazio vuoto oppure ci saranno altri numeri? Ecco, oggi immaginiamo di avere una bella lente di ingrandimento e andiamo a scoprire cosa c’è in quello spazio!” Erano molto curiosi: che razza di lente di ingrandimento si sarà portata da casa maestra Michela? “Bambini, siamo tutti d’accordo che il nostro intero equivale a una unità? E che 10 un’unità valgono una decina? Bene… adesso andiamo a comprendere quanto varrà un decimo“. Faccio notare ancora una volta che la matematica è una materia astratta che però, per aiutarci a comprendere, si avvale di simboli numerici ma anche di schemi e immagini. Le frazioni ci aiuteranno a comprendere quei valori più piccoli di una unità. Per noi è semplice immaginare e comprendere immediatamente a quanto corrisponda il simbolo 1, stessa cosa vale per il 10. Se io chiedo di prendere una penna o 10 penne, o anche di immaginarle, nessuno manifesta alcuna difficoltà. Ma un decimo di penna cosa significa? “Maestra, dovremmo dividere una penna in 10 parti più piccole e prenderne un pezzetto!“. Capirete bene che a questo punto dobbiamo ricorrere a qualche “artifizio”: le frazioni. Con le frazioni cerchiamo di comprendere ciò che sta dietro (per ora senza far riferimento ai numeri razionali o ai rapporti tra interi) i numeri decimali… ossia diversi da quelli interi (per ora avevamo esplorato solo numeri naturali interi). Partiamo quindi dalla consapevolezza che un decimo è sicuramente più piccolo di una unità e vediamo con l’immagine dell’intero frazionato perché.
Ho chiesto di prendere in considerazione solo una decima parte di quell’intero e di nominarlo. Dopo di che, andando alla lavagna nera, ho disegnato una linea dei numeri così come l’abbiamo sempre conosciuta: inizia da 0, prosegue in ordine crescente con numeri interi, potrebbe continuare all’infinito. “Ma vi siete mai chiesti cosa accade in quell’intervallo che va dallo 0 all’1? Noi lo vediamo. Ci sarà uno spazio vuoto oppure ci saranno altri numeri? Ecco, oggi immaginiamo di avere una bella lente di ingrandimento e andiamo a scoprire cosa c’è in quello spazio!” Erano molto curiosi: che razza di lente di ingrandimento si sarà portata da casa maestra Michela? “Bambini, siamo tutti d’accordo che il nostro intero equivale a una unità? E che 10 un’unità valgono una decina? Bene… adesso andiamo a comprendere quanto varrà un decimo“. Faccio notare ancora una volta che la matematica è una materia astratta che però, per aiutarci a comprendere, si avvale di simboli numerici ma anche di schemi e immagini. Le frazioni ci aiuteranno a comprendere quei valori più piccoli di una unità. Per noi è semplice immaginare e comprendere immediatamente a quanto corrisponda il simbolo 1, stessa cosa vale per il 10. Se io chiedo di prendere una penna o 10 penne, o anche di immaginarle, nessuno manifesta alcuna difficoltà. Ma un decimo di penna cosa significa? “Maestra, dovremmo dividere una penna in 10 parti più piccole e prenderne un pezzetto!“. Capirete bene che a questo punto dobbiamo ricorrere a qualche “artifizio”: le frazioni. Con le frazioni cerchiamo di comprendere ciò che sta dietro (per ora senza far riferimento ai numeri razionali o ai rapporti tra interi) i numeri decimali… ossia diversi da quelli interi (per ora avevamo esplorato solo numeri naturali interi). Partiamo quindi dalla consapevolezza che un decimo è sicuramente più piccolo di una unità e vediamo con l’immagine dell’intero frazionato perché.
Ritornando alla linea dei numeri allora posizioniamo il nostro intero sopra la linea. L’intero corrisponde alla quantità 1. Sono tutti d’accordo? Dopo aver disegnato alla LIM e sul quaderno sì.
 Vediamo che l’intero-unità occupa l’intervallo tra lo 0 e 1. Ma noi questo intero l’abbiamo frazionato in 10 parti e allora andiamo con il rosso a segnare le tacche in quell’intervallo che vogliamo scoprire con la nostra ipotetica lente di ingrandimento. “Bambini, dopo lo zero… nella prima tacca che valore numerico dovremmo inserire? Unità ce ne sono?” – “Le unità per ora sono zero, maestra. E poi c’è quel pezzettino!” Quel pezzettino è un decimo quindi diciamo che abbiamo 0 unità e un decimo (una decima parte di unità) ossia 0,1. Guardando i pezzetti di intero presi via via… capiscono subito come proseguire: ogni pezzo contato ci consente di proseguire in ordine crescente verso destra. Contiamo tutte le tacche e arriviamo a 10 esattamente nel punto dove si trova l’1! “Perché?”- “Perché abbiamo preso tutte le 10 parti. 10/10 sono infatti l’intero ossia l’unità”. Questo l’hanno scoperto loro… ma incalzo: “E dopo come si prosegue?“. Capiscono intuitivamente che si prosegue come hanno sempre fatto ma adottando una strategie diversa che include anche la virgola. Osserviamo che 1/10 è come dire 1:10 ossia 0,1. Facciamo qualche esempio (riprendendo anche le strategie per dividere gli interi per 10, 100 e 1000) per intuire cosa c’è dietro lo spostamento verso la parte sinistra della cifra “togliendo” gli zeri o, adesso, introducendo la virgola. Questo aspetto lo vedremo ancora meglio con lo strumento molto intuitivo presente nella Linea del 1000 di Bortolato che aiuta anche all’esecuzione delle equivalenze tra misure. Per ora ci fermiamo qui e ci appuntiamo quanto scoperto: i numeri oltre la virgola. In questa giornata inseriamo anche il centinaio… perché i bambini erano curiosi di capire allora cosa c’è nell’intervallo tra lo 0 e lo 0,1. Anche quell’intervallo sarà diviso per 10. Se lo prendiamo dentro l’intero scopriamo che siamo all’interno di un intero frazionato in 100 parti (10 X10): siamo nella zona dei centesimi. Lo scriviamo ma lo vediamo nello specifico in un altro momento. Per questa volta ci basta riassumere quanto visto così:
Vediamo che l’intero-unità occupa l’intervallo tra lo 0 e 1. Ma noi questo intero l’abbiamo frazionato in 10 parti e allora andiamo con il rosso a segnare le tacche in quell’intervallo che vogliamo scoprire con la nostra ipotetica lente di ingrandimento. “Bambini, dopo lo zero… nella prima tacca che valore numerico dovremmo inserire? Unità ce ne sono?” – “Le unità per ora sono zero, maestra. E poi c’è quel pezzettino!” Quel pezzettino è un decimo quindi diciamo che abbiamo 0 unità e un decimo (una decima parte di unità) ossia 0,1. Guardando i pezzetti di intero presi via via… capiscono subito come proseguire: ogni pezzo contato ci consente di proseguire in ordine crescente verso destra. Contiamo tutte le tacche e arriviamo a 10 esattamente nel punto dove si trova l’1! “Perché?”- “Perché abbiamo preso tutte le 10 parti. 10/10 sono infatti l’intero ossia l’unità”. Questo l’hanno scoperto loro… ma incalzo: “E dopo come si prosegue?“. Capiscono intuitivamente che si prosegue come hanno sempre fatto ma adottando una strategie diversa che include anche la virgola. Osserviamo che 1/10 è come dire 1:10 ossia 0,1. Facciamo qualche esempio (riprendendo anche le strategie per dividere gli interi per 10, 100 e 1000) per intuire cosa c’è dietro lo spostamento verso la parte sinistra della cifra “togliendo” gli zeri o, adesso, introducendo la virgola. Questo aspetto lo vedremo ancora meglio con lo strumento molto intuitivo presente nella Linea del 1000 di Bortolato che aiuta anche all’esecuzione delle equivalenze tra misure. Per ora ci fermiamo qui e ci appuntiamo quanto scoperto: i numeri oltre la virgola. In questa giornata inseriamo anche il centinaio… perché i bambini erano curiosi di capire allora cosa c’è nell’intervallo tra lo 0 e lo 0,1. Anche quell’intervallo sarà diviso per 10. Se lo prendiamo dentro l’intero scopriamo che siamo all’interno di un intero frazionato in 100 parti (10 X10): siamo nella zona dei centesimi. Lo scriviamo ma lo vediamo nello specifico in un altro momento. Per questa volta ci basta riassumere quanto visto così:
“Mi raccomando bambini, in questi giorni rivedete il lavoro sul quaderno e continuate a pensare a quanto scoperto in queste settimane… perché la settimana prossima vi vorrei presentare la Rana Romilda… e non vorrebbe mai cogliervi impreparati!” Chi sarà mai questa Rana Romilda? Ma non è che la maestra porta in classe una rana vera??? Per alcuni giorni abbiamo continuato a lavorare con le frazioni e i numeri decimali sia sul libro di testo delle Discipline sia sulla Linea del 1000. Abbiamo utilizzato anche lo strumento e eseguito una serie di esercizi atti a farci familiarizzare con le virgole. Il lavoro con frazioni e numeri decimali è stato anche rinforzato grazie all’euro. Infatti andando a perlustrare quanto già appreso gli anni scorsi sull’euro (abbiamo lavorato con banconote e monete scoprendo il meccanismo di funzionamento anche grazie a semplici situazioni problematiche proposte nella linea del 100, lezione per scoperta sull’euro e al mercatino in classe) ci è stato possibile richiamare alla memoria quanto scoperto in seconda. Un euro a questo punto diventa la nostra unità, l’intero, e i centesimi sono le frazioni di quell’intero. Ci aiutiamo con esempi pratici, disegniamo l’intero frazionato il cento parti e analizziamo a quanto equivale la parte frazionaria al numero decimale e alla moneta dei centesimi di euro. Di grande aiuto, sia per impatto visivo che per gli esercizi semplici e mirati (che trovano poi riscontro sul libro) è il software della linea del 1000.
 Finalmente arriva il giorno della Rana Romilda! Per raccogliere queste settimane di esperienza diretta con frazioni e numeri decimali ho infatti escogitato un percorso un po’ particolare (non so come mi sia venuta l’idea!) ma che ha suscitato grande interesse. Notando quanto sia stato semplice far acquisire il concetto di numero decimale a partire dall’intero frazionato collocato sopra la linea dei numeri… ho inventato una semplice storia che mi ha consentito di consolidare quanto appreso, scoprire altri aspetti sin’ora passati inosservati e verificare le competenze dei bambini. La protagonista di questa storia è la Rana Romilda e non me la sono certo inventata io. E’ stato il genio Bruno Munari (intellettuale, ecletico artista-designer, disegnatore, creativo, visionario e chi più ne ha più ne metta) a inventare la Rana Romilda, protagonista proprio del racconto omonimo. Il mio amore per Bruno Munari ha radici lontane: la mia seconda tesi di laurea “Letture in gioco: parole e immagini per creare”. Nella mia tesi Munari e Rodari sono i protagonisti indiscussi e molte delle idee che mi balenano per la testa si sviluppano proprio grazie al grande estro di questi Maestri. Preparando la tesi ho acquistato una marea di libri di Bruno Munari (ce ne sono di disparati… se ancora non li conoscete andateli a cercare e resterete ammaliati perché ogni libro è fonte di ispirazione e offre davvero l’opportunità di sviluppare lezioni incredibili)… tra cui La Rana Romilda. A differenza di altri suoi testi, questo è un racconto su albo illustrato. A causa della sua abitudine di saltare di palo in frasca, Romilda si imbatte in una serie di avventure curiose e incredibili, combinandone di tutti i colori!Per farla conoscere ai miei alunni ho portato in classe il libro presentando l’autore e la Rana ma ho poi deciso di mostrare loro (per mancanza di tempo ma anche per garantire un’attenzione più vigile) un breve video trovato sul web. Il filmato, creato da una scuola dell’infanzia, racconta in maniera semplificata la storia della Rana Romilda direttamente dalla voce dei bambini e dalle loro creazioni in plastilina.
Finalmente arriva il giorno della Rana Romilda! Per raccogliere queste settimane di esperienza diretta con frazioni e numeri decimali ho infatti escogitato un percorso un po’ particolare (non so come mi sia venuta l’idea!) ma che ha suscitato grande interesse. Notando quanto sia stato semplice far acquisire il concetto di numero decimale a partire dall’intero frazionato collocato sopra la linea dei numeri… ho inventato una semplice storia che mi ha consentito di consolidare quanto appreso, scoprire altri aspetti sin’ora passati inosservati e verificare le competenze dei bambini. La protagonista di questa storia è la Rana Romilda e non me la sono certo inventata io. E’ stato il genio Bruno Munari (intellettuale, ecletico artista-designer, disegnatore, creativo, visionario e chi più ne ha più ne metta) a inventare la Rana Romilda, protagonista proprio del racconto omonimo. Il mio amore per Bruno Munari ha radici lontane: la mia seconda tesi di laurea “Letture in gioco: parole e immagini per creare”. Nella mia tesi Munari e Rodari sono i protagonisti indiscussi e molte delle idee che mi balenano per la testa si sviluppano proprio grazie al grande estro di questi Maestri. Preparando la tesi ho acquistato una marea di libri di Bruno Munari (ce ne sono di disparati… se ancora non li conoscete andateli a cercare e resterete ammaliati perché ogni libro è fonte di ispirazione e offre davvero l’opportunità di sviluppare lezioni incredibili)… tra cui La Rana Romilda. A differenza di altri suoi testi, questo è un racconto su albo illustrato. A causa della sua abitudine di saltare di palo in frasca, Romilda si imbatte in una serie di avventure curiose e incredibili, combinandone di tutti i colori!Per farla conoscere ai miei alunni ho portato in classe il libro presentando l’autore e la Rana ma ho poi deciso di mostrare loro (per mancanza di tempo ma anche per garantire un’attenzione più vigile) un breve video trovato sul web. Il filmato, creato da una scuola dell’infanzia, racconta in maniera semplificata la storia della Rana Romilda direttamente dalla voce dei bambini e dalle loro creazioni in plastilina.
A questo punto vi starete chiedendo: ma si parla di frazioni? scopre i numeri decimali? incontra un matematico strampalato? Niente di tutto ciò. La storia con le frazioni l’ho inventata io… molto semplicemente. Romilda è la protagonista perché essendo una rana… salta e questa volta ha saltato nella nostra linea dei numeri 😉 compiendo le sue avventure. Il percorso ci ha consentito di procedere alla scrittura posizionale dei numeri razionali sulla linea dei numeri. Il numero razionale 1/10 è la “particella” mediante la quale possiamo passare a un livello a destra rispetto alla posizione dell’1 partendo dallo 0. Per fare 1, abbiamo visto, servono infatti 10 decimi!). L’unità rappresenta il viaggio che compie la Rana Romilda e i decimi sono le tappe che si susseguono prima che arrivi a destinazione. Ecco la prima parte della pagina LIM.
Alla LIM ho predisposto la consegna (ascolta la storia, disegna, rappresenta e ragiona…) e la storia distribuita pezzo per pezzo. I bambini hanno come riferimento visivo i paragrafi della storia alla LIM che verrà letta loro passo passo. Nei loro quaderni rappresentano sulla linea dei numeri ciò che accade favorendo i ragionamenti, la disposizione dei numeri e la risposta dei quesiti finali grazie anche alle immagini gancio. Ad ogni pezzetto di storia ha corrisposto una parte del percorso e i ragionamenti: io alla LIM (ma anche loro chiamati per completare le parti) e loro sul quaderno. Inizialmente ho letto il primo pezzo di storia e ho spiegato ai bambini che avremmo trovato un nuovo modo per “riassumere” il nostro racconto: non avremo usato parole ma bensì immagini, schemi e numeri. Abbiamo disegnato la nostra linea dei numeri da 0 a 1 (0 la partenza e 1 il traguardo) e poi disegnato le immagini gancio. Poi, ragionando sul percorso abbiamo sistemato le tacche dei dieci salti e ragionato sul fatto che ogni salto fosse un decimo di percorso (o unità). Abbiamo proseguito con la storia  e dopo aver letto tutti i paragrafi ho chiesto di disegnare una nuova linea dei numeri per segnare le tappe della rana ragionando di volta in volta, inserendo le immagini gancio e i termini frazionari. Ci hanno aiutato anche i colori. Io alla LIM e loro sul quaderno. La prima tappa l’abbiamo fatta insieme mentre le successive le hanno sistemate loro per primi sui loro quaderni e io dopo alla LIM come verifica e confronto del lavoro.
e dopo aver letto tutti i paragrafi ho chiesto di disegnare una nuova linea dei numeri per segnare le tappe della rana ragionando di volta in volta, inserendo le immagini gancio e i termini frazionari. Ci hanno aiutato anche i colori. Io alla LIM e loro sul quaderno. La prima tappa l’abbiamo fatta insieme mentre le successive le hanno sistemate loro per primi sui loro quaderni e io dopo alla LIM come verifica e confronto del lavoro.
A questo punto abbiamo focalizzato la nostra attenzione sul percorso completando con le informazioni raccolte:
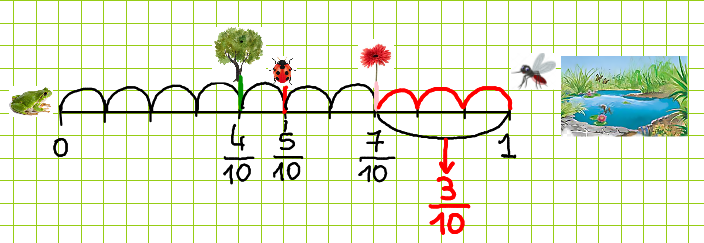
I bambini hanno scritto le frasi predisposte da me alla LIM e completato in autonomia inserendo i termini frazionari. Infine ho deciso di chiedere quanto mancasse, sempre in termini frazionari, alla conclusione del percorso e loro hanno risposto prontamente e in coro “3/10!”. Ho colto l’occasione per parlare loro della frazione complementare e ragionarci un po’ su. Infine ho proposto di raccontare anche con i numeri decimali come abbiamo imparato ad inserire sulla linea dei numeri e sempre tenendo come riferimento i numeri frazionari. Questo ci ha consentito di ripassare una delle nostre ultime lezioni e ritornare ancora una volta al concetto di unità e decimi di unit. Ecco il lavoro sul loro quaderno:
Per concludere la nostra attività ho impostato una semplice tabella per raccogliere i dati della nostra avventura e avere a portata d’occhio termini frazionari e numeri decimali. Con questo semplice schema i bambini hanno avuto la possibilità di vedere ancora una volta lo stretto legame tra frazioni decimali e numeri decimali. Ho impostato il lavoro in questo modo e ho chiesto loro di completare a casa inserendo tutte le tappe sino ai 10/10 ossia l’intero percorso.